
Shape optimization.
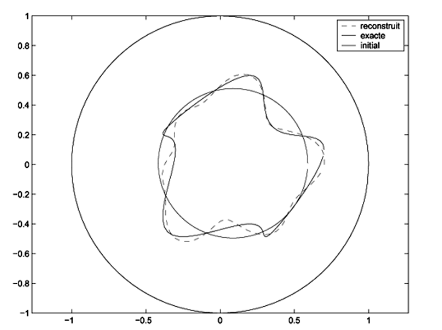
Inverse problems.
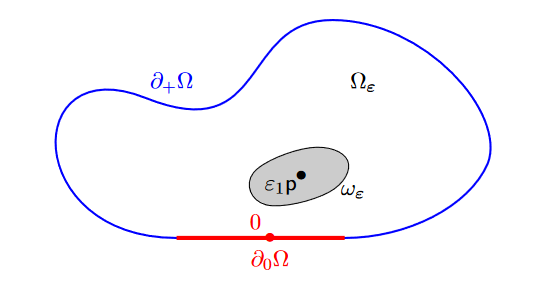
Asymptotic analysis of the solution of PDEs
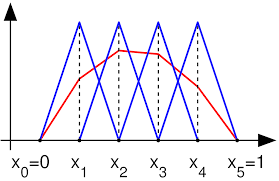
Numerical analysis of PDEs.
Optimization in finite dimension.
Shape Optimization
Optimization in finite dimension
Numerical analysis of PDEs
Inverse problems
PDEs and asymptotic analysis of solutions of PDEs
 Shape optimization. |
 Inverse problems. |

Asymptotic analysis of the solution of PDEs |
 Numerical analysis of PDEs. |
|---|---|
 Optimization in finite dimension. |